Ein routine-integrierbares Planungswerkzeug zur operativen Rekonstruktion der Orbita

 Thomas M. Deserno ¹
Wei Liao ¹
Marc C. Metzger ²
Melanie E. H. Kleiner ¹
Dirk Schulze <sup>2

1</sup> Institut für Medizinische Informatik, RWTH Aachen, Deutschland
² Universitätsklinik für Zahn-, Mund- und Kieferheilkunde (ZMK), Klinik für Mund-, Kiefer- und Gesichtschirurgie, Plastische Operationen, Universität Freiburg, Deutschland

Zusammenfassung

Bei der operativen Rekonstruktion des Orbitabodens ist unter anderem die Gleichheit von linkem und rechten Orbitavolumen für das Sehvermögen entscheidend. In dieser Arbeit wird ein Planungswerkzeug entwickelt, welches mit Hilfe eines aktiven Konturmodells den Orbitainhalt in CT-Datensätzen segmentiert, ihr Volumen berechnet und dieses visualisiert, um dem operierenden Arzt die Therapieplanung und -kontrolle zu erleichtern. Neben den technischen Integrationsstufen der Funktions- und Präsentationsintegration, die durch den Einsatz des Medical Imaging Interaction Toolkit (MITK) direkt erreicht werden, sowie der Daten-, und Kontextintegration, die durch das DICOM Protokoll unterstützt werden, ist vor allem die Stabilität, Robustheit und Korrektheit der eingesetzten Algorithmen für die Routine-Integrierbarkeit wichtig.

Stabilitätsuntersuchungen bei 20 Patienten und jeweils 50 zufällig gewählten Startpunkten zeigen einen mittleren Variationskoeffizienten von 0,72%, d.h. deutlich unterhalb der kritischen 5% Schwelle. Die Robustheitsuntersuchung auf 200 Orbitae ergab eine Fehlerrate von 8%. Vergleiche der Volumina der rechten und linken Seite bei 74 klinisch unauffälligen Individuen resultiert in einem mittleren Variationskoeffizienten von 0,85%, so dass das Verfahren auch als korrekt angesehen werden kann. Exemplarisch wird die Anwendbarkeit mit einer klinischen Fallstudie belegt.

Aufgrund der nachgewiesenen Stabilität und Korrektheit des Verfahrens sowie der umgesetzten Daten-, Funktions-, Kontext- und Präsentationsintegration kann das Tool in den klinischen Prozess eingebunden werden, und soll nun in der praktischen Anwendung umfassend evaluiert werden.

---

1 Einleitung

Frakturen des Orbitabodens sind eine der häufigsten Frakturen in der Gesichts- und Kieferchirurgie [1]. Um die Sehfähigkeit weitestgehend wiederherzustellen, wird bei einer in der klinischen Erprobung befindlichen Methode operativ ein Titangitter in Höhe des Orbitabodens eingesetzt. Es wird davon ausgegangen, dass das rekonstruierte Volumen dabei eine entscheidende Rolle spielt. Die Operationsplanung kann also durch eine robuste prä- und postoperative Volumenberechnung anhand von computertomographischen (CT) Daten sowie einer geeigneten Visualisierung entscheidend und effizient unterstützt werden [2].

Für die Segmentierung dreidimensionaler (3D) CT-Daten existieren viele Methoden [3]. Daten-, pixel- oder regionenbasierte Verfahren, wie die Watershed-Transformation, sind aber nicht in der Lage, Lücken in der Kontur zu schließen und Artefakte bei der CT-Darstellung der dünnen Orbita-Knochen zu kompensieren. Deshalb wurden in der Vergangenheit oft modellbasierte Segmentierungsmethoden eingesetzt. Lamecker et al. [4] zerlegen die knöchernen Strukturen, die die Orbita begrenzen, in sechs Teilbereiche, für die jeweils ein statistisches Formmodell trainiert wird. Von Klinski et al. [5], [6] verwenden anatomische Spline-Modelle, die an die jeweiligen Organe innerhalb der Orbita angepasst werden, und so die aufgrund von Artefakten fehlende Information kompensieren können. Derartige Modelle, die vor allem in der Strahlentherapie von Tumoren zum Einsatz kommen, können die große Variabilität frakturierter Orbitae nicht erfassen. Deswegen werden auch in der aktuellen klinischen Forschung immer noch manuelle Segmentierungsmethoden eingesetzt [7].

Aktive Konturmodelle hingegen liefern immer eine geschlossene Kontur und können sehr unterschiedliche Formvarianten erkennen. Die Segmentierung der Orbita wird daher mit einem diskreten, aktiven Konturmodell durchgeführt. Das von Bredno et al. [8] vorgeschlagene Verfahren hat gegenüber anderen Implementierungen eine Reihe von Vorteilen:

1. Die Stützstellen des aktiven Modells liegen nicht innerhalb der einzelnen 2D-Schichten, sondern werden während der Iteration beliebig im 3D-Raum platziert;
2. Die Kräfte, die auf die Stützstellen des aktiven Modells wirken, werden nicht nur an der Position einer Stützstelle selbst sondern aus der gesamten triangulierten Oberflächenumgebung der beteiligten Stützstellen berechnet;
3. Eine konstante Ballonkraft modelliert das Aufblasen einer physikalischen Membran, so dass die teilweise schwierige Initialisierung beim klassischen Snake-Ansatz entfällt.

Die Lösung des Segmentierungsproblems alleine ist jedoch nicht ausreichend, um prä- und post-operative Unterstützung in der klinischen Routine zu leisten [9]. Die robuste Parametrierung, Stabilität und Korrektheit sind weitere Grundvoraussetzungen für die Integrierbarkeit des Planungswerkzeugs in die medizinische Routine [10]. Hierzu gehört auch die Möglichkeit des Anwenders, das Segmentierungsergebnis zu kontrollieren [9]. In diesem Beitrag wird dargestellt, wie mit Hilfe des Medical Imaging Interaction Toolkits (MITK), das am Deutschen Krebsforschungszentrum (DKFZ) in Heidelberg entwickelt wird [11], ein routine-integrierbares Planungswerkzeug zur operativen Rekonstruktion der Orbita erstellt wurde.

2 Material und Methoden

Zunächst werden die zur Planung der operativen Rekonstruktion der Orbita erforderlichen Arbeitsschritte modelliert:

1. Einlesen der Bilddaten
2. Initialisierung
3. Segmentierung
4. Visualisierung
5. Volumenbestimmung
6. Spiegelung und Seitenvergleich
7. Simulation eines Gittereinsatzes

Diese Funktionen wurden mit MITK abgebildet [11]. Das MITK verbindet das Insight Segmentation and Registration Toolkit (ITK; http://www.itk.org) mit dem Visualization Toolkit (VTK; http://www.vtk.org) und ist besonders für Endanwendungen in der klinischen Praxis geeignet [12]. Zusätzlich bietet MITK eine Standardapplikation, in die auf einfache Weise eigene Module eingebettet werden können, sowie Klassen zur Interaktion des Benutzers mit den Bilddaten. Durch die Datenhaltung in einer Baumstruktur können unterschiedliche Strukturen in Relation zueinander dynamisch verwaltet und gleichzeitig in verschiedenen Ansichten konsistent angezeigt werden.

Für die Routine-Integrierbarkeit ist neben der eigentlichen Verfügbarmachung der Bildverarbeitungsalgorithmen sowie den Kontrollmöglichkeiten für den Anwender, welche durch eine geeignete Interaktion realisiert werden können, vor allem die Stabilität und Korrektheit des Verfahrens wichtig, was methodisch sauber untersucht werden muss [9]. Hierzu standen CT-Datensätze von 100 Probanden ohne Frakturen der Orbita zur Verfügung.

2.1 Segmentierung der Orbita

2.1.1 Orbitaabschluss

Für die Segmentierung der Orbita, die als Hohlraum frontal nicht durch Knochen abgegrenzt wird, ist die Definition einer Begrenzung nach vorne notwendig. In dieser Arbeit wurden drei Methoden realisiert, die in ähnlicher Weise bereits in anderen Arbeiten zur manuellen oder semi-automatischen Bestimmung des Orbitavolumens zur Anwendung kamen [13], [14], [15]. Zunächst wird als Begrenzung der frontale Übergang zwischen Gewebe und Luft verwendet. Dies geschieht bereits durch die Vorverarbeitung, indem Hounsfieldeinheiten kleiner als 400 weiß gefärbt werden und damit wie Knochen als externe Einflüsse des Modells wirken.

Die beiden anderen Methoden gehen von einer segmentierten Kontur bis zu dieser Grenze aus und schneiden entlang einer Ebene weitere Bereiche vor der Orbita weg. Eine Variante bestimmt zunächst eine Hauptachse dieser Kontur, die frontal aus der Orbita herausragt und verschiebt dann an dieser entlang eine Ebene zum Schädel hin bis drei Stützpunkte, die untereinander einen Mindestabstand besitzen, bestimmt werden konnten (Abbildung 1 [Abb. 1]). An diesen wird dann die endgültige Abschlussebene ausgerichtet. Somit entstehen auf beiden Seiten unterschiedlich geneigte Ebenen.

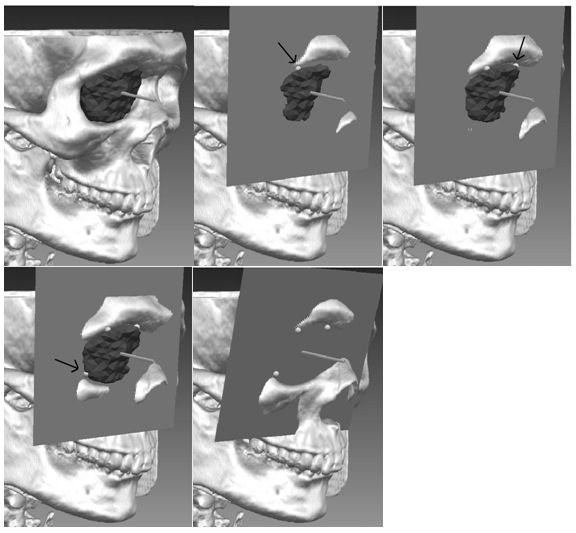
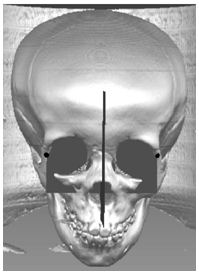
Die dritte Methode bestimmt anhand der Augapfelmittelpunkte eine zur Symmetrieachse senkrecht gelegene Abschlussebene, die beide Jochbeine auf Höhe der Augapfelmittelpunkte verbindet (Abbildung 2 [Abb. 2]). Weitere Methoden, um die Orbita zu schließen, sind denkbar und können einfach integriert werden. In der Literatur hat sich bisher keine Variante für die Orbitavolumenbestimmung durchgesetzt. Einerseits muss der Abschluss klar definiert sein, andererseits muss er der Vorstellung, die Mediziner von dem Volumen der Orbita entwickelt haben, im Wesentlichen entsprechen.

2.1.2 Aktive Kontur-Segmentierung

Die Segmentierung verwendet das aktive Konturmodell nach Bredno et al. [8]. Eine konstante Ballonkraft modelliert physikalisch das Aufblasen einer Membran, die lediglich im Inneren der Orbita liegen muss (siehe Abschnitt 2.1.3) und durch die Bildgradienten an den knöchernen Strukturen aufgehalten wird, bis sie schließlich die Form der gesuchten Orbita hat und die Iteration konvergiert ist. Die Parameter des Ballonmodells wurden wie folgt bestimmt:

• Applikationsspezifische Parameter: Die externen Einflüsse leiten sich von den Bildinformationen ab. Beim Laden eines CT-Datensatzes werden die Grauwerte in Hounsfield Einheiten (HE) umgerechnet, die abhängig von der Dichte des Gewebes aber unabhängig von individuellen Geräteeinstellungen oder der Lage des Patienten sind. Die DICOM-Tags „Rescale Slope“ (0028,1053) und „Rescale Intercept“ (0028,1052) enthalten die zur Umrechnung relevante Information. Damit können die Gradienten im Bild applikationsspezifisch zunächst für die einzelnen Kanten der Kontur bestimmt und dann auf die jeweiligen Stützstellen umgerechnet werden. Die globalen Einflüsse (Ballonkraft) wirken abhängig von der Größe der zugehörigen Kanten auf jeden Knoten in Richtung der Summe der Normalen der zugehörigen Kanten.
• Bildspezifische Parameter: Im DICOM-Header der CT-Daten ist auch die Größe eines Voxels in realen Maßen abgelegt. Die Tags „Pixel Spacing“ (0028,0030) und „Slice Thickness“ (0018,0050) geben den physikalischen Abstand in x- und y- Richtung bzw. in z-Richtung in mm an. Über die so ermittelte Schichtdicke kann ein isotropes Konturenmodell berechnet werden.
• Iterationsspezifische Parameter: Die internen Einflüsse (Deformationskraft) dienen dazu, die Kontur insgesamt zu glätten. Die Deformationskraft wirkt unterschiedlich stark, abhängig davon, wie groß die aktive Kontur gerade ist, denn bei einer kleinen kugelförmigen Kontur sind die Winkel zwischen den Kanten größer, als bei einer großen Kontur mit mehr Knoten mit derselben Form. Da bei der Segmentierung der Orbita eine starke Deformationskraft notwendig ist, um ein Herauslaufen an Lücken zu verhindern, eine zu starke Deformationskraft im Anfangsstadium aber zu einem Schrumpfen der Kontur führen kann, wurde die Deformationskraft iterationsspezifisch gesetzt. Sie steigt linear mit der Knotenzahl an. Diese kontinuierliche Steigerung der Deformationskraft führt außerdem zu einer verbesserten Konvergenz, da eine herauslaufende Kontur, je größer sie wird, immer stärker durch Deformationskräfte zurückgehalten wird und somit selbst bei fehlenden Bildinformationen die Ballonkraft aufheben kann.

2.1.3 Startpunktwahl

Um den Startpunkt für die Segmentierung automatisch zu finden, wurde die von ITK implementierte 2D-Hough-Transformation für eine Verwendung im Dreidimensionalen erweitert. Die Bildung eines Gradientenbildes entfällt, stattdessen wird eine Fensterung von 40–50 HE (Blut) vorgenommen, da der Augapfel nur außen stark durchblutet ist und somit eine geeignete kugelförmige Kante bereits durch die geeignete Fensterung entsteht (Abbildung 3 [Abb. 3]).

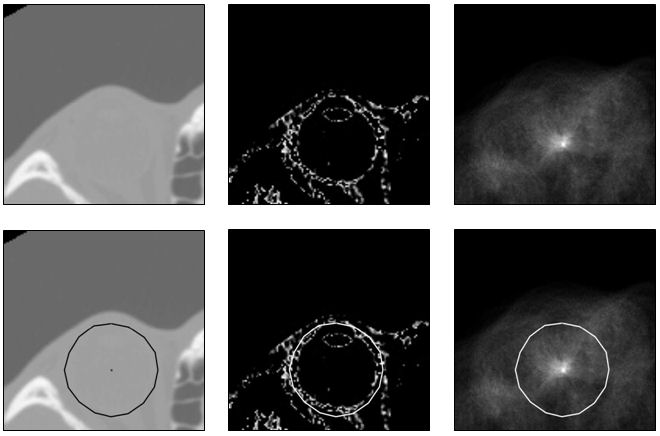
Der für die Hough-Transformation benötigte Radius wurde konstant auf 12 mm gesetzt. Bei einer Bestimmung des Volumens des Augapfels anhand von CT-Daten in [16], wurden bei Patienten über zwei Jahren Volumina zwischen 6,41 cm³ und 9,80 cm³ berechnet, welche einem Radius von 11,52 mm bis 13,28 mm entsprechen. Auch in [17] werden an erwachsenen Augen Durchmesser zwischen 22 mm und 27 mm und damit Radien zwischen 11 mm und 13,5 mm gemessen. Dabei ist zu berücksichtigen, dass in den CT-Bildern nur die äußeren Schichten des Augapfels, Lederhaut (Sklera), Aderhaut (Choroidea) und Netzhaut (Retina), als Kontur sichtbar sind. Diese Schichten sind laut [18] durchschnittlich 1,3 mm dick. Eine Kugel mit einem Radius von 12 mm lässt sich also robust in Patienten ab zwei Jahren einpassen.

2.2 Integration

Zunächst lässt sich die Integration einzelner Module zu einem System auf verschiedenen Ebenen untersuchen [19]:

1. Datenintegration bedeutet, dass das Planungswerkzeug auf die Daten im PACS Archiv direkt zugreifen kann. Dies ist über das verwendete Digital Imaging and Communication in Medicine (DICOM) Protokoll möglich.
2. Funktionsintegration bedeutet, dass das Werkzeug von der Arbeitsstation des Anwenders aufrufbar ist. Da MITK auf plattformunabhängigen Komponenten aufsetzt, kann das Programm sowohl auf Windows- als auch auf Linux/Unix-Rechnern betrieben werden.
3. Präsentationsintegration bedeutet, dass Oberfläche und Bedienung vergleichbar zu Standardmodulen auf dem Computer des Anwenders ist. Auch dies ist durch den Einsatz von MITK gegeben.
4. Kontextintegration bedeutet, dass der Zusammenhang (z.B. Patient) zwischen den Applikationen (z.B. Befundungssoftware und Planungswerkzeug) automatisch ausgetauscht wird. Hierfür stehen proprietäre Schnittstellen der Befundungssoftware zur Verfügung.

2.3 Stabilität

Stabilität bedeutet, dass für eine klinische Situation immer der gleiche Messwert ermittelt wird, unabhängig von leichten Variationen in der Verfahrensparametrierung und den (manuellen) Komponenten bei der Initialisierung. Das Planungswerkzeug muss zum einen die Stabilität in Bezug zum gewählten Startpunkt, zum anderen die stabile Schließung der Orbita, und zuletzt die stabile Segmentierung bei unterschiedlichem Bildmaterial gewährleisten.

Stabilität kann dabei mit dem Variationskoeffizienten v erfasst werden, der als statistische Kenngröße die relative Standardabweichung, d.h. die Standardabweichung σ dividiert durch den Mittelwert μ einer Zufallsvariablen X beschreibt. In der Regel wird der Variationskoeffizient in Prozent angegeben:

v = σ / μ

Die Motivation für diesen Kennwert ist, dass eine Zufallsvariable mit großem Mittelwert im Allgemeinen eine größere Varianz aufweist als eine mit einem kleinen Mittelwert. Da die Varianz und damit die Wurzel daraus, die Standardabweichung, nicht normiert sind, kann im Allgemeinen nicht beurteilt werden, ob eine Varianz groß oder klein ist.

Der Startpunkt kann mit der in Abschnitt 2.1.3 beschriebenen Hough-Transformation automatisch bestimmt werden. Ein semi-automatisches Verfahren, das den manuellen Startpunkt noch einmal verschiebt, ist ebenfalls integriert. Die Parameterstabilität insgesamt wird mit folgendem Experiment überprüft:

• Hypothese: Das Verfahren ist unabhängig von der Wahl der Initialisierung und den adaptiven Parametern.
• Durchführung: In 20 zufällig ausgewählten Datensätzen wird die Initialisierung an jeweils 50 zufällig bestimmten Voxeln innerhalb der Orbita durchgeführt und das Volumen bestimmt.
• Ergebnis: Das Verfahren wird als hinreichend stabil angesehen, wenn der Variationskoeffizient v<5% ist [9]

2.4 Robustheit

Die individuelle Anatomie, Frakturen oder Artefakte sowie unterschiedliche Aufnahmemodalitäten und -einstellungen können dazu führen, dass das Segmentierungsverfahren fehlschlägt. Dies kann mit einer visuellen Plausibilitätsanalyse überprüft werden. Das entsprechende Experiment wurde wie folgt gewählt:

• Hypothese: Das Verfahren ist robust.
• Durchführung: Für 200 Orbitae wird die Segmentierung durchgeführt. Manuell werden die Ergebnisse überprüft, und die Anzahl der Fehldetektionen wird ermittelt.
• Ergebnis: Das Verfahren wird als hinreichend robust angesehen, wenn die Fehlerrate <5% ist [9].

2.5 Korrektheit

Korrekt ist eine Segmentierung genau dann, wenn sie mit der tatsächlichen Kontur übereinstimmt. Allerdings ist die Ground-Truth bei den realen Datensätzen nicht bekannt. Deshalb wurde bei 74 klinisch unauffälligen und visuell plausibel segmentierten Patienten das Volumen der rechten und linken Seite miteinander verglichen.

• Hypothese: Das Volumen der rechten und linken Seite ist gleich groß.
• Durchführung: In allen klinisch unauffälligen und visuell plausibel segmentierten Patienten wird das Volumen rechts und links bestimmt. Der frontale Abschluss wird einmal anhand der Luft/Gewebe-Grenze und einmal mit der gemeinsamen Ebene bestimmt.
• Ergebnis: Das Verfahren wird als hinreichend korrekt angesehen, wenn der Variationskoeffizient v<5% ist [9].

3 Ergebnisse

3.1 Planungswerkzeug

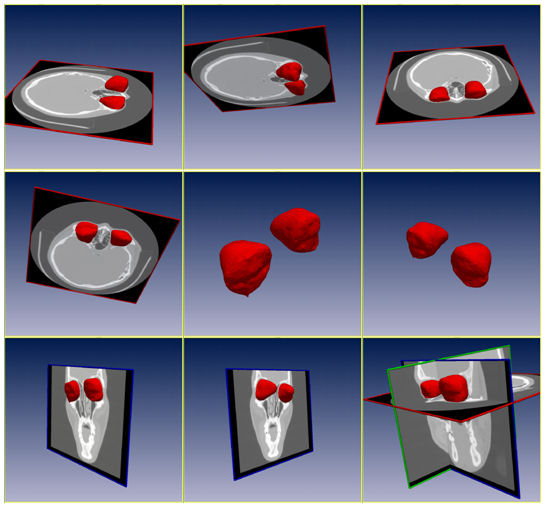
In dem entwickelten Planungswerkzeug wurden alle Arbeitsschritte zur Planung der operativen Rekonstruktion der Orbita realisiert. CT-Daten können vom Benutzer geladen und betrachtet werden. Eine manuelle Startpunktwahl wie auch eine semi-automatische Initialisierung durch automatische Verschiebung auf die Bulbusmitte sind implementiert, sodass der Segmentierungsprozess gestartet, und die Segmentierung als Oberfläche betrachtet werden kann. Das Volumen wird auf beiden Seiten berechnet und gegenübergestellt (Abbildung 4 [Abb. 4]). Die Segmentierung kann gespiegelt und ein Gitter eingefügt werden. Nachdem das Gitter an die gewünschte Stelle verschoben, gedreht und ggf. verformt wurde, kann eine neue Segmentierung unter Berücksichtigung des Gitters als Grenze erfolgen. Mit Standard-Komponenten des MITK lassen sich die Daten auch als Volumen visualisieren, Distanzen messen, sowie einzelne Achsen, Teilsegmentierungen oder Ähnliches ein- und ausblenden (Abbildung 5 [Abb. 5]).

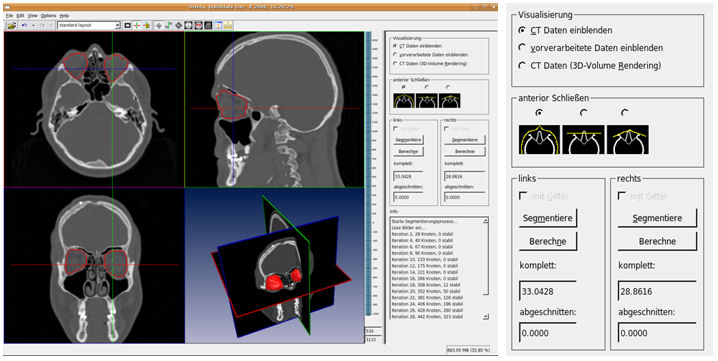
3.2 Evaluierung

Bei dem Stabilitätstest betrug der durchschnittliche Variationskoeffizient 0,72%. Die Ergebnisse der visuellen Plausibilitätsprüfung sind in Tabelle 1 [Tab. 1] dargestellt. Danach sind 8,00% der 200 Orbitae nicht zufrieden stellend segmentiert worden. Bei dem Vergleich der rechten und linken Orbitavolumina wurde ein mittlerer Variationskoeffizient von 0,85% für die Segmentierung mit dem Luft/Gewebe-Übergang als frontalen Abschluss und ein mittlerer Variationskoeffizient von 2,74% bei einem frontalen Abschluss mittels gemeinsamer Ebene festgestellt.

3.3 Fallstudie

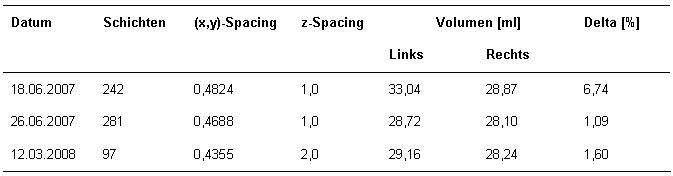
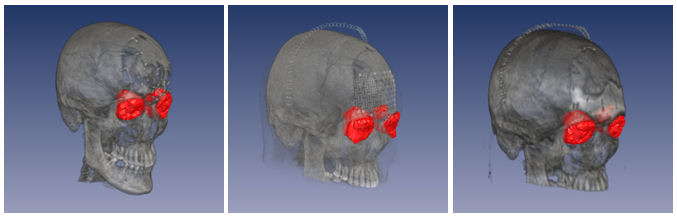
Tabelle 2 [Tab. 2] zeigt die Ergebnisse an drei unabhängigen CT-Daten eines 41-jährigen Patienten, bei dem Orbita und Stirn nach einer operativen Erstversorgung nach Verkehrsunfall in einem zweiten Eingriff mit einem Titangitter rekonstruiert wurden, welches dann später nochmals durch ein Keramikimplantat ersetzt wurde (Abbildung 6 [Abb. 6]). Die Volumendifferenzen nach Erstversorgung sind zu groß, so dass der Patient auch weiterhin über Sehprobleme klagte. Mittels Titangitter konnte hinsichtlich der Orbitavolumenrekonstruktion ein fast optimales Ergebnis erzielt werden: die Differenz zwischen linkem und rechten Volumen liegt bei 1%. Dieses Ergebnis wurde auch nach dem Austausch des Gitters mit einem Keramikimplantat erhalten.

4 Diskussion

Die Stabilität und die Korrektheit des Verfahrens konnte in einer Validierungsstudie belegt werden, da der Variationskoeffizient im Mittel deutlich unter 5% lag. Die Überprüfung der Robustheit mittels visueller Plausibilitätsprüfung ergab eine Fehlerrate von 8%, die laut Evaluationsprotokoll als zu groß angesehen werden muss. Für eine objektive Beurteilung der Segmentierungen fehlen Referenzkonturen, mit denen die Segmentierungen verglichen werden könnten.

Der Rechts-/Links-Volumenvergleich von Orbitapaaren ergab für den natürlichen Luft/Gewebe-Abschluss sowie den Abschluss durch eine gemeinsame Ebene jeweils einen Variationskoeffizienten deutlich kleiner als 5%. Die Volumina weichen also nicht mehr voneinander ab, wie bei einem hinnehmbaren Messfehler derselben Orbita. Problematisch ist bei dem Rechts-/Links-Vergleich aber die Tatsache, dass sich auch bei gesunden, intakten Schädeln das Volumen der beiden Augenhöhlen um bis zu 8% unterscheiden kann [20].

Das Volumen selbst wird in [21] bei Probanden, die älter als ein Jahr sind, so dass das Auge als ausgewachsen angesehen werden kann, im Bereich von 20 bis 30 cm³ angegeben. Von Watzek hat basierend auf 50 mazerierten Schädeln (ohne Berücksichtigung der Geschlechtszugehörigkeit) das Orbitavolumen mit 27,28 ± 2,54 cm³ angegeben [22]. Dies entspricht unseren Messungen in den 100 CT-Daten sowie auch in der Fallstudie (Tabelle 2 [Tab. 2]).

Es kann somit festgehalten werden, dass alle Arbeitsschritte zur Planung der operativen Rekonstruktion der Orbita erfolgreich in ein Planungswerkzeug integriert werden konnten, welches nun wertvolle Informationen und Möglichkeiten bietet, um das Orbitavolumen von Patienten zu messen und zu beurteilen. Die beidseitige Spiegelung der Segmentierung sowie der virtuelle Einsatz eines Gitters schließen die Funktionalität des Planungswerkzeuges ab, das nun der medizinischen Forschung zur Verfügung steht.

Anmerkung

Interessenkonflikte

Keine angegeben.

---

Literatur

[1] Shere JL, Boole JR, Holtel MR, Amoroso PJ. An analysis of 3599 midfacial and 1141 orbital blow out fractures among 4426 United States Army Soldiers, 1980-2000. Otolaryngology. 2004;130(2):164-70.
[2] Scolozzi P, Jaques B. Computer-aided volume measurement of posttraumatic orbits reconstructed with AO titanium mesh plates: accuracy and reliability. Ophthal Plast Reconstr Surg. 2008;24(5): 383-9. DOI: 10.1097/IOP.0b013e318185a72c
[3] Masero V, León-Rojas JM, Moreno J. Volume reconstruction for health care: a survey of computational methods. Ann N Y Acad Sci. 2002;980:198-211. DOI: 10.1111/j.1749-6632.2002.tb04897.x
[4] Lamecker H, Kamer L, Wittmers A, Zachow S, Kaup T, Schramm A, Noser HR, Hammer B. A method for the three-dimensional statistical shape analysis of the bony orbit. Proc Computer Aided Surgery Around the Head. 2007;94-7.
[5] Von Klinski S, Glausch A, Derz C, Tolxdorff T. Modellbasierte Rekonstruktion von Organoberflächen auf der Basis von zweidimensionalen Schnittdaten. In: Evers H, Glombitza G, Lehmann T, Meinzer HP, editors. Bildverarbeitung für die Medizin 1999. Berlin: Springer; 1999. p. 312-6.
[6] Von Klinski S. Modellbasierte Auswertung von dreidimensionalen Schnittbilddaten der Orbita [Dissertation]. Berlin: Freie Universität, Fachbereich Mathematik und Informatik; 2001.
[7] Regensburg NI, Kok PH, Zonneveld FW, Baldeschi L, Saeed P, Wiersinga WM, Mourits MP. A new and validated CT-based method for the calculation of orbital soft tissue volumes. Invest Ophthalmol Vis Sci. 2008;49(5):1758-62. DOI: 10.1167/iovs.07-1030
[8] Bredno J, Lehmann TM, Spitzer K. A general discrete contour model in 2, 3 and 4 dimensions for topology-adaptive multi-channel segmentation. IEEE Trans Pattern Anal Mach Intell. 2003;25(5):550-63. DOI: 10.1109/TPAMI.2003.1195990
[9] Lehmann TM. Digitale Bildverarbeitung für Routineanwendungen. Wiesbaden: Deutscher Universitätsverlag; 2005.
[10] Udupa JK, Leblanc VR, Zhuge Y, Imielinska C, Schmidt H, Currie LM, Hirsch BE, Woodburn J. A framework for evaluating image segmentation algorithms. Comput Med Imaging Graph. 2006;30(2):75-87. DOI: 10.1016/j.compmedimag.2005.12.001
[11] Wolf I, Vetter M, Wegner I, Böttger T, Nolden M, Schöbinger M, Hastenteufel M, Kunert T, Meinzer HP. The medical imaging interaction toolkit. Med Image Anal. 2005;9(6):594-604. DOI: 10.1016/j.media.2005.04.005
[12] Bitter I, Uitert RV, Wolf I, Ibanez L, Kuhnigk JM. Comparison of four freely available frameworks for image processing and visualization that use ITK. IEEE Trans Vis Comput Graph. 2007;13(3):483-93. DOI: 10.1109/TVCG.2007.1001
[13] Bite U, Jackson IT, Forbes GS, Gehring DG. Orbital volume measurements in enophthalmos using three-dimensional CT imaging. Plast Reconstr Surg. 1985;75:502-8.
[14] Whitehouse RW, Batterbury M, Jackson A, Noble JL. Prediction of enophthalmos by computed tomography after 'blow out' orbital fracture. Br J Ophthalmol. 1994;78:618-20. DOI: 10.1136/bjo.78.8.618
[15] Koppel DA, Foy RH, McCaul JA, et al. The reliability of "analyze" software in measuring orbital volume utilizing ct-derived data. J Craniomaxillofac Surg. 2003;31:88-91. DOI: 10.1016/S1010-5182(02)00170-1
[16] Hahn FJ, Chu WK. Ocular volume measured by CT scans. Neuroradiology. 1984;26:419-20.
[17] Perkins ES. Ocular volume and ocular rigidity. Exp Eye Res. 1981;33:141-5. DOI: 10.1016/S0014-4835(81)80062-0
[18] Wilmer HA, Scammon RE. Growth of the components of the human eyeball; I Diagrams, calculations, computation and reference tables. Arch Ophthal. 1950;43:599-619.
[19] Winter A, Ammenwerth E, Brigl B, Haux R. Krankenhausinformationssysteme. In: Lehmann TM, editor. Handbuch der Medizinischen Informatik. München: Hanser; 2005.
[20] Parsons GS, Mathog RH. Orbital wall and volume relationships. Arch Otolaryngol Head Neck Surg. 1988;114:743-7.
[21] Hingst V, Knaape A, Schnittkowski M, Hauenstein KH, Guthoff R. Zur Methodik und Genauigkeit der MR-Volumetrie der Orbita. Klin Monatsbl Augenheilkd. 2004;221:894-7. DOI: 10.1055/s-2004-813357
[22] Von Watzek G. Vergleichende anatomisch-röntgenologische Untersuchungen der knöchernen Orbita und des Neurokraniums. Fortschr Kieferorthop. 1978;39(4):265-73. DOI: 10.1007/BF02225784